Better Master Passwords: The geek edition

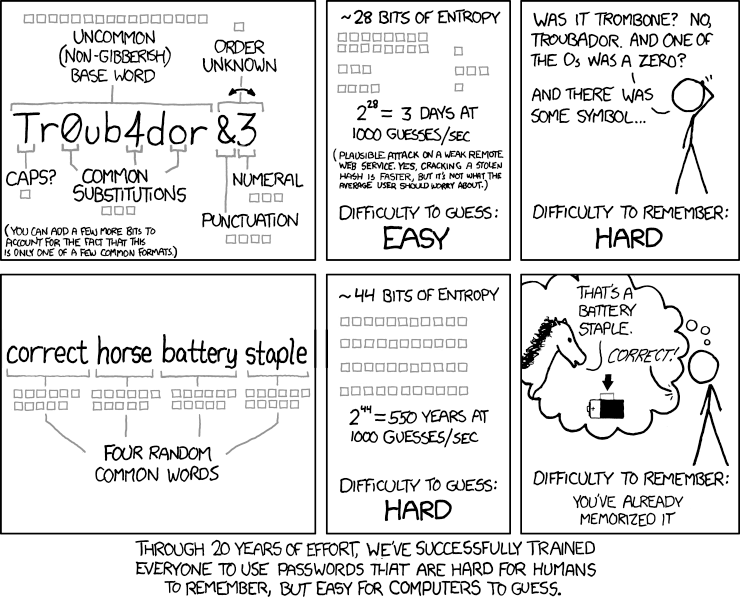
Indeed, what took me nearly 2000 words to say in non-technical terms, Randall Monroe was able to sum up in a comic. This just shows the power of math, but that’s another issue. So for those of you who want to understand the comic and see how it relates to my earlier post, read on. But first read or re-read my earlier post on strong master passwords.

If, like most sane people, you don’t want to dive into a technical discussion, then stop here and just read the original, non-technical, post that says the same thing as the comic. It’s also where the practical advice is.

The only thing I’ll restate

There is one concept (well, actually two concepts) from the Toward Better Master Passwords post that needs to be restated. It is central to everything that follows:

The strength of a password creation system is not how many letters, digits, and symbols you end up with, but how many ways you could get a different result using the same system.

This embodies two things that we need to take into account when looking at the strength of some components of security. Kerchoff’s Principle, and entropy.

Kerchoff’s Principle

Kerchoff’s Principle states that you should assume that your adversary knows as much about the system you use as you do. In this case it means that if you are following advice about how to generate strong memorable passwords, the people who will be trying to break that password are at least as familiar with that advice as you are.

I can’t over-emphasize the point that we need to look at the system instead of at a single output of the system. Let me illustrate this with a ridiculous example. The passwords F9GndpVkfB44VdvwfUgTxGH7A8t and rE67AjbDCUotaju9H49sMFgYszA each look like extremely strong passwords. Based on their lengths and the use of upper and lower case and digits, any password strength testing system would say that these are extremely strong passwords. But suppose that the system by which these were generated was the following: Flip a coin. If it comes up heads use F9GndpVkfB44VdvwfUgTxGH7A8t, and if it comes up tails use rE67AjbDCUotaju9H49sMFgYszA.

That system produces only two outcomes. And even though the passwords look strong, passwords generated by that system are extremely weak. Of course nobody would recommend a system that only produced two outcomes, but people do recommend systems that produce a far more limited number of outcomes than one might think by inspecting an individual result of the system. This is because humans are far more predictable than we like to believe.

Entropy

What unit do we use to measure the number of different results you can get from a system? The answer to that is “bits of entropy”. The silly system I listed above can get us two different results. We can represent two different outcomes using one binary digit (bit). Passwords from that system have just one bit of entropy.

Now suppose we had a similar system that involved rolling one die. That would lead to six possibilities. Six outcomes can be represented in three bits (with a little room to spare). The actual number of bits is closer to 2.58. (And for those who really want to know where that number came from it is the base-2 logarithm of 6.)

One feature of using bits of entropy as a measure is that each bit represents a doubling of the number of possible outcomes. Something with 10 bits of entropy represents 1024 possibilities, while 11 bits will double that to 2048 possible outcomes. There are many reasons that we use bits instead of the number of possibilities. I won’t go into the mathematical reasons, but one nice result is that it gives us manageable numbers. In cryptography we routinely deal with things that have 128 bits of entropy. 128-bits would represent 340282366920938463463374607431768211456 possible outcomes. It’s hard think about or compare such numbers.

Working through the comic

Now lets look at a few things in the first pane of the comic. Let’s start with the stuff I’ve put into the green pink box. The single small gray square in the bottom of the green pink box shows that the choice between capitalizing or not capitalizing the word adds one bit of entropy. Of course people could add more entropy by possibly capitalizing other letters, but people don’t capitalize randomly. The do so at the beginning, at the end, or sometimes at internal word or syllable boundaries.

If people capitalized randomly that would add a lot of entropy, but capitalizing randomly would make the password impossible to remember.

Now let’s look at the stuff that I’ve put in the blue box. Here 16 bits are awarded to picking an uncommon, but non gibberish word. That would imply that the person picked a word in a truly random fashion from a list of “2 to the power of 16” words (65536). I don’t believe that people would be truly random in their choice of base words, so I would assign fewer bits to this choice, but I’m not going to quibble about a few bits here and there.

The red box covers three “tricks”. Adding some punctuation and a numeral to the end of the password. Adding a numeral gives us roughly four bits of additional entropy, and punctuation gives us four. We get one additional bit by not knowing which comes first, the digit or the punctuation. I didn’t put a box around the common substitutions and misspellings of changing something like Troubadour to Tr0b4dor; three additional bits seems about right.

When we add up all of the bits of entropy that this system uses we get 28-bits. Of course the system can be made more complex and may go up a few bits, but almost certainly at a great cost of memorability.

For those who recall some laws of logarithms, you now can see an additional benefit for using bits as our unit instead of numbers of possible outcomes: We can add the bits contributed by each choice instead of having to multiply the number of possibilities. It is very convenient to say that such-and-such adds X bits of entropy.

Now contrast this with using a sequence of random common words. It is absolutely crucial that the words be chosen in a truly random fashion. Here 11 bits are assigned to each word. That means that the list of common words used has “2 to the power of 11” elements. That is, it is from a word list of 2048 words. This gives a more memorable password with 44 bits of entropy.

Cracking time

Depending on what sort of access the bad guys have, they can test from 1000 passwords per second to hundreds of thousands per second. For more information on how we slow this down, see the post on PBKDF2. Only you can decide how much effort someone will put into cracking your master password if they get hold of your data.

Using Diceware alone with five words (you know what I’m talking about because you read the earlier post) you will get 64 bits of entropy. If you add your own private scheme (say it contributes 10 bits) then you will have 74 bits of entropy, which would take about 500 million years to crack at one million guesses per second. Not everyone needs that kind of strength in a master password.

Of course if you do have Three Letter Agencies willing to spend hundreds of millions of dollars specifically on getting at your secrets, then you have problems bigger than what can be managed through software alone. Indeed, let me point you to another favorite xkcd comic.

[Updated: August 11 to correct my colorblindness error and spelling of Randall Munroe’s name. — jpg]

Jeffrey Goldberg

Principal Security Architect