You may have heard some news going around about hashcat, a password cracking tool, that recently increased its ability to guess Master Passwords for 1Password data files. It’s an impressive achievement for hashcat, and it is important to understand what this does and doesn’t mean for 1Password.
What you need to know
1Password has not been “cracked”
The existence of a new cracking tool (actually there is another new tool, but only the hashcat one is getting much attention due to its speed) does not mean that anything is broken in 1Password. Indeed, the fact that we are open about our design is one of our strengths. Hashcat’s remarkable guessing speeds is the real news here.
Your Master Password is your protection
This development only highlights what we’ve said all along: your Master Password is your defense and you need to pick a strong Master Password. Our measures to slow down automated guessing helps a great deal, but they are no substitute for a great Master Password.
Is there a flaw? Well, yeah. It’s complicated
The announcement said that some of hashcat’s speed achievements is due to a flaw in the design of the Agile Keychain Format. Indeed, there is a very subtle flaw. Exactly how much the flaw contributes to their cracking speed is something I’ll talk about below. In short, it contributes—literally—one bit. But more on that later.
There are a couple of technical misunderstandings about the flaw that I’d like mention here in our “cliff notes introduction”, but with the details and explanation to come further below.
- We didn’t call PBKDF2 twice during key derivation (that would be silly). However, we called PDBDF2 once in a way that had the effect of calling it twice. That is still a flaw because it has the identical result of doing something silly, but it was a non-silly flaw.
- Hashcat was able to reduce the number of hash calls fourfold. But our flaw was only half of that. The other half is not specific to 1Password.
Terrific community
Understanding the precise nature of the “flaw” and related issues was a communal effort involving hashcat developers, John the Ripper developers, cryptographers, and members of the information security community. The debate, discussion, questioning, and explaining within this community is fantastic. Some the debate continues and not everyone involved will agree with every point of the more detailed assessment below.
More background
Ready for the next level of detail? Here goes.
Password crackers and how to defend against them

Password crackers, such as John the Ripper and hashcat, are tools that automate password guessing. Over the past year, they have turned their attention to password managers, including 1Password. This doesn’t reflect a weakness in password managers in any way. Indeed, I think the fact that we were among the first to draw this sort of attention is to our credit. The question isn’t whether someone has tools to automate password guessing—we should always assume that they do—but how many guesses can be checked in a short period of time. The faster they can guess, the stronger people’s passwords need to be.
Naturally, we have put in measures to make password guessing slow. We use PBKDF2, which requires that there be lots of computations to go from an entered Master Password to actually unlocking your 1Password data. Then the question is about how good a job our use of PBKDF2 does against these highly optimized tools. The short answer is that PBKDF2 helps enormously, but it is no substitute for a strong Master Password. When we get to the technical discussion (if you stick with me that far), you will learn a great deal more about PBKDF2.
What does this mean for my Master Password?
For a couple thousand dollars today, an attacker can build a machine that will guess millions of 1Password Master Passwords per second. So let’s look at how long it would take for that to crack various types of Master Passwords, assuming the scenario of an attacker getting a copy of your Agile Keychain and setting this machine to work on nothing other than guessing your Master Password.


For the numbers I give, I’m going to pretend that you all created Master Passwords using the scheme in Toward Better Master Passwords, called “diceware.” It’s not because I actually assume that everyone is using that system, but we need to know how strong a password is (measured in bits of entropy) to perform calculations about how long it might take to guess them. It is remarkably hard to know how strong a password is just by counting letters, digits, and symbols. Instead you need to understand the system that was used to create the password.
If you have a three word diceware password with 1Password using 10000 PBKDF2 iterations, the hashcat machine (more on that in a bit) would have a 50% chance of running through all three word-long diceware passwords in about nine days. If you use a four word password then it would take almost 200 years. At five words, it would take 1.5 million years. With six words and above we are talking about billions of years.
What about increasing PBKDF2 iterations?
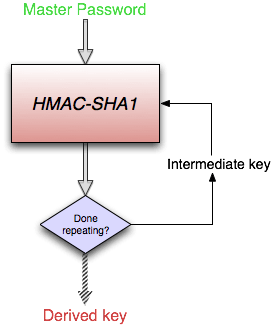
The very first versions of the Agile Keychain Format long ago used 1000 PBKDF2 iterations. More recently, when a new keychain is created or the Master Password changed (in version 3.9 for Mac), we changed that to a minimum of 10000 iterations (and possibly more depending on your system). It is tempting to think that we should just increase these numbers dramatically. We will certainly be looking at increasing that minimum, but it is very important to understand that increasing the number of PBKDF2 iterations stops paying off after a while. We reach a point where there is far greater security improvement for the effort making a Master Password stronger than there is for increasing the number of PBKDF2 iterations.
I’m going to talk about the security of Master Passwords in terms of bits of entropy. You don’t need understand the details other than to know that each additional bit doubles the cracking time. So if you have a Master Password that has 40 bits of entropy (basically that there are 2⁴⁰ different alternatives passwords you could have created using the same password creation system) it might take, say, 100 years to crack under certain conditions. If it were one bit more (41 bits) then it would take 200 years to crack under the same circumstance.
We can also double the amount of time to crack by doubling the number of PBKDF2 iterations. Going from 10000 iterations to 20000 doubles the crack time, and so it adds the equivalent of 1 bit to the effective strength. Going from 1000 PKDF2 iterations to 10000 PBKDF2 iterations (increasing the iterations 10 times) effectively adds about 3.3 bits of entropy. The attacker needs to work 10 times harder. If you go from 10000 iterations to 20000 iterations, you only gain one additional bit. The attacker only needs to work twice as hard. Going from 20000 iterations to 30000 iterations gives about 0.6 bits of additional strength.
Now contrast adding a single randomly chosen lowercase letter to your password. Each one will add 4.7 bits of entropy. That would be like going from 10000 PBKDF2 iterations to 260000 iterations. Adding another randomly chosen lowercase letter would add additional 4.7 bits, but trying to do the same by increasing PBKDF2 iterations would now take us to 6.7 million iterations. Adding a diceware word to your master password will add 13 bits.
To get the same effect as adding a diceware word by adding PBKDF2 iterations would mean going from 10000 PBKDF2 iterations to 78 million iterations. With that, it would probably take more than an hour or two to unlock your 1Password data on an iPhone if the effort didn’t entirely drain the battery first. The simple lesson is that once we have a few tens of thousands of PBKDF2 iterations, increasing them doesn’t add much security, while it does add to real costs to the legitimate user of the data. The more effective route is to spend a second or two typing a longer password instead of having PBKDF2 spend a few seconds exhausting your battery.
Beyond diceware
The Master Password generation scheme that I recommend in Toward Better Master Passwords involves picking words from a list of 7776 words by rolling dice. We can make these passwords stronger by using a longer list of words. The reason that 7776 is that it works by rolling five dice (or one die five times). We can use a longer word list if we don’t need to roll dice. But it is absolutely essential for the security of the scheme that the process of picking words is really random and not under direct human control.
Another option is to do as I suggested in that article. Create a relatively short password the usual (not very good way), but make sure it isn’t something on the diceware list. Then create a diceware password and simply add the two together.
A third, more complicated option, is something that is a bit of a “work in progress”, but this hashcat news means we can talk about it a little early. The idea is to use lists of words from different languages as well as longer lists of words. Randomly pick which language to use for your first word, then use diceware on that. You may have to learn a few foreign words in the process, but once you’ve learned those words they should be about as easy to remember as the words of your native language.
I have prepared lists of words exactly for this scheme along with a README file that contains not fully fleshed out instructions on how to use the system. This is very experimental, but it has allowed me to have a a strong Master Password for 1Password on iOS which isn’t too annoying to type on an iPhone keyboard or to remember.
The really technical details
I was definitely impressed to learn that they are getting three million trials per second against 1Password data that used 1000 iterations for PBKDF2. It is important to understand how. There were four things that gave them a speed up, and I’ll work from the least (smallest speed up) to the most significant. I should note that some people I have enormous respect for do not fully agree with my assessment. If you’d like to dive into this, please follow the discussion on the hashcat forums.
But first, another word about PBKDF2
Three of the four mechanisms I discuss involve the inner workings of PBKDF2. So we need to peek a bit more into that black box. PBKDF2 takes something like a password and transforms that password over and over again and eventually spits out a big number (a string of bits). When you call PBKDF2, you not only tell it how many iterations it should run through, but you also tell it what function should be used to transform the data in each round. The function has to be what is called a “pseudo-random function”, but other than that PBKDF2 doesn’t insist on much. We say that PBKDF2 “is constructed” from a PRF.
The PRF that is typically used with PBKDF2 is HMAC. I’ve written about HMAC before. Now HMAC is constructed from a hash function, and a number of different hash functions will work. Different hash functions give different size output. SHA1 gives 20 bytes of output. SHA256 gives 32 bytes, and SHA512 gives 64 bytes of output. If you call SHA1 but only need 16 bytes of output you just take the first 16 bytes of of the 20 byte output and throw away the rest. This is called “truncating”.
The hash functions we use are constructed from “compression functions”. Compression functions are designed to be fast, but they are still where the real computation takes place. So the idea of PBKDF2 is to require that the underlying compression function is computed many times.
All of these concepts and constructions will play a role in the discussion of points 2, 3, and 4 below. But first, to the one that has nothing to do with PBKDF2.
1. Only one AES block needs be decrypted per guess
When data is encrypted using a block cipher (such as AES) in CBC mode with standard padding, the attacker doesn’t need to decrypt each block of ciphertext to see if things “work”. The attacker only needs to decrypt the final block. This is not anything particularly new, but it is an important optimization. This way, the attacker needs only one AES decryption per guess.
An aside to any application developers: It is perfectly fine for an attacker to use this shortcut, but applications should never, ever, ever, use this trick as a way to report decryption success or failure. Really. Don’t do it.
Again, I believe (but haven’t confirmed) that other crackers running against CBC mode use the same optimization. It’s an optimization, but a typical one and doesn’t represent a flaw. We want the slowdown to take place in PBKDF2.
2. PBKDF2-HMAC optimization
There is a neat trick that can be used to speed up PBKDF2-HMAC calculations by a factor of two. I first saw this trick in John the Ripper, and it is used here in hashcat as well. Now this optimization, however, is available to defenders as well as to attackers. So if our use of PBKDF2 uses the same trick as is used in hashcat and John the Ripper then this comes out as a tie between Attacker (them) and Defender (us).
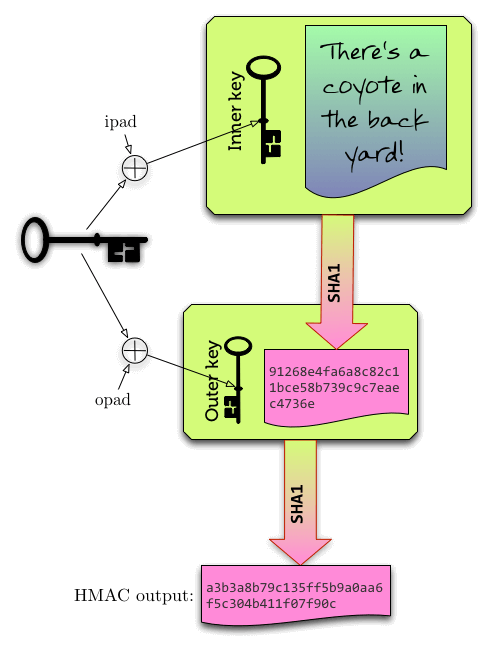
PBKDF2 calls HMAC for each iteration. Each run of HMAC normally involves two hashing operations. Each of those two hashing operations involve two compressions. So we have four compressions altogether for each call to HMAC. However, two of those compressions are going to be exactly the same (with the same data) for each PBKDF2 iteration. If we compute those two compressions only once and save those results, then we can cut down the computation needed for each PBKDF2 round in half.
This optimization of PBKDF2-HMAC-SHAn is available to both the attacker and to the defender. So this only really counts as a “speed up” for the attacker if the defender isn’t using it and isn’t taking it into account when calibrating the number of PBKDF2 iterations. So does 1Password use this optimization? It depends on the particular software libraries we use. I believe (but haven’t received confirmation from Apple on this yet) that the PBKDF2 implementation in CommonCrypto does do this. I don’t believe that the cryptographic library we use for 1Password for Windows does, which might help explain why unlocking 1Password on Windows takes a bit longer than it does on the Mac. Indeed, we’ve been looking at using our own custom PBKDF2 implementation on Windows specifically to get this optimization.
3. Don’t ask more of PBKDF2 than it is ready to give
This is where the design flaw in the Agile Keychain key derivation mechanism. We ask PBKDF2 to give us 32 bytes of data, but we also tell it to use HMAC-SHA1. This, combined with the fact that we used one half of its output for one thing and the other half for another, is our misdesign.
SHA1 only produces 20 bytes of data and so if we ask PBKDF2-HMAC-SHA1 for 32 bytes of data it can’t run its natural course. Instead what it does (with some rounding and truncating) is run PBKDF1 (which gives at most 20 bytes of output) twice. Once to produce the first 16 bytes that we asked for and once to produce the second 16 bytes of output. If we asked it 10000 iterations, it will actually run through 20000 iterations, 10000 to produce the first part of the output and 10000 to produce the second part of the output. This is a fact about PBKDF2 that we were not aware of at the time.
Normally this behavior of PBKDF2 wouldn’t be a problem, as both the attacker and the defender would suffer from an equal slowdown of twice as many calls to the underlying hash function. But, in the words of Mr Monk, here’s the thing. We used the first 16 bytes that output as a derived AES key and the second 16 bytes as an initialization vector. The password guesser only needs the AES key to see if a password works. To actually decrypt the data, the IV is needed as well, but it is possible for the candidate password to be verified with only the AES key.
Splitting the output of PBKDF2 is a perfectly fine thing to do. Asking for more data from PBKDF2 that you’d natively get from the hash you give it should also be fine. After all, that is something that PBKDF2 was designed to handle. But doing both of those turns out to allow an attacker to do just half of the work that you need to do when you run PBKDF2.
Without this flaw, the guess rate would still be 3 million guesses per second for 1000 PBKDF2 iterations. It just means that our own use of PBKDF2 would “cost” half as much and so that we could double the number of iterations.
4. Really, really well designed GPU processing

Hashcat does many things well, but I think that what they really excel at is GPU processing and parallelization. Their ability to spread out all of the work among four GPUs and have each one perform SHA1 computations very quickly is, I believe, where the real speed is.
The compression functions (invoked by the hash functions, invoked by HMAC, invoked by PBKDF2) happen to run really nicely on GPUs, and all of the constructions build on top of them also have nothing in them that presents difficulties for highly optimized code on GPUs. So roughly speaking, PBKDF2 provides no meaningful defense against parallel computation, and its typical components can be implemented very very nicely on GPUs.
Beyond PBKDF2
As we look at the above list, we see that three of them involve design features of PBKDF2. PBKDF2 is not serving its purpose as well as we would want. Now I love PBKDF2. It may not be engraved on my heart, but it is engraved on my iPad. But it has been growing clearer that the world needs a successor to PBKDF2. A possible successor, scrypt, does consume memory as well a CPU (or GPU). But PBKDF2, scrypt, and the search for a successor will have to be the topic of a separate article. Indeed, it is the subject of the article that I would have been working on today had not the hashcat announcement come.
We continue to use PBKDF2 in our new data format, but with some important changes. First of all, we use SHA512 which makes it safe for us to ask for 64 bytes of data that we do split into halves. Also our use of SHA512 should make things more difficult for GPU-based crackers. Exactly how difficult remains to be seen.
Our next steps
Quite simply it is far too early to promise specific changes in response to this. Changing the key derivation system in the Agile Keychain isn’t something that can be done quickly, as we would need to make sure that 1Password on every single platform we support would be ready for the change before we started converting data files. I’m not ruling that out; but it would take a great deal of time, be fraught with compatibility issues, and would only save one bit worth of effective password strength.
We could boost the number of PBKDF2 iterations, but as described above, we’ve reached a point of diminishing returns for that. It will probably happen slowly and behind the scenes, as it has done in the past.
We can make certain that all our PBKDF2 implementations perform the HMAC-PBKDF2 optimization. We were already in the process of doing this when the hashcat news broke.
We can advise people on creating stronger Master Passwords, as that has and continues to be your best protection. Indeed, we will continue to do so as we also explore ways to make it easier for people to create and use such passwords.
[Update 1: At the moment, changing your Master Password will only recalibrate the number of PBKDF2 iterations when you use 1Password 3.9 on the Mac. We will have further information about 3.8 and 1Password on other platforms shortly.]
[Update 2: PBKDF2 settings for different versions of 1Password.
Calibration requires something introduced in OS X 10.7 (Lion) and iOS 5. So calibration is only available in the Mac App Store version of 1Password for Mac (which requires OS X 10.7) and in 1Password 4 for iOS (which requires iOS 6). 1Password for Windows, 1Password for Mac 3.0-8, and 1Password 3 on iOS do not calibrate.
- 1Password 3.9 Mac: All versions of 1Password for Mac from the Mac App Store (MAS) calibrate the number of PBKDF2 iteration on initial set up and on Master Password change. A minimum of 10000 iterations is used.
- 1Password 4 iOS: All versions of 1Password 4 for iOS calibrate the number of PBKDF2 iteration on initial set up and on Master Password change. A minimum of 10000 iterations is used.
- Mac 1Password 2.5.0 (October 2007) – 3.8.10: Keychains were created using 1000 PBKDF2 iterations.
- Mac 1Password 3.8.11 (December, 2011) – 3.8.20: Keychains were created using 10000 PBKDF2 iterations. Changing the Master Password did not change iterations.
- Mac 1Password 3.8.21 (April 2013): Keychains are created using 10000 PBKDF2 iterations. On a Master Password change, iterations will be increased from 1000 to 10000 if necessary.
- Windows 1Password 1.0.0.36 (April 2010) – 1Password 1.0.9.296: Keychains created with 1000 PBKDF2 iterations.
- Windows 1Password 1.0.9.299 (October 2012) – 1Password 1.0.9.327: Keychains created with 10000 PBKDF2 iterations. Master Password change does not increase number of iterations.
- Windows 1Password 1.0.9.328 (May 2013): Keychains are created using 10000 PBKDF2 iterations. On a Master Password change, iterations will be increased from 1000 to 10000 if necessary.
Please note that that making a small improvement to your Master Password has a far far greater effect than making a large increase in the number of PBKDF2 iterations.]
[Update 3: 1Password and hashcat: The Movie.
I presented on this at PasswordsCon in Las Vegas on Juny 31, 2013. Per Thorsheim, one of the organizers of the conference, has uploaded videos of the talks.
But really, you would be better off watching the other talks from PasswordsCon. You already know what I have to say. The other talks were fantastic. You can also get the PDF slides for that presentation.]

 by Jeffrey Goldberg on
by Jeffrey Goldberg on


Tweet about this post